Right Triangle Hypotenuse Calculator
Hypotenuse: 0.00
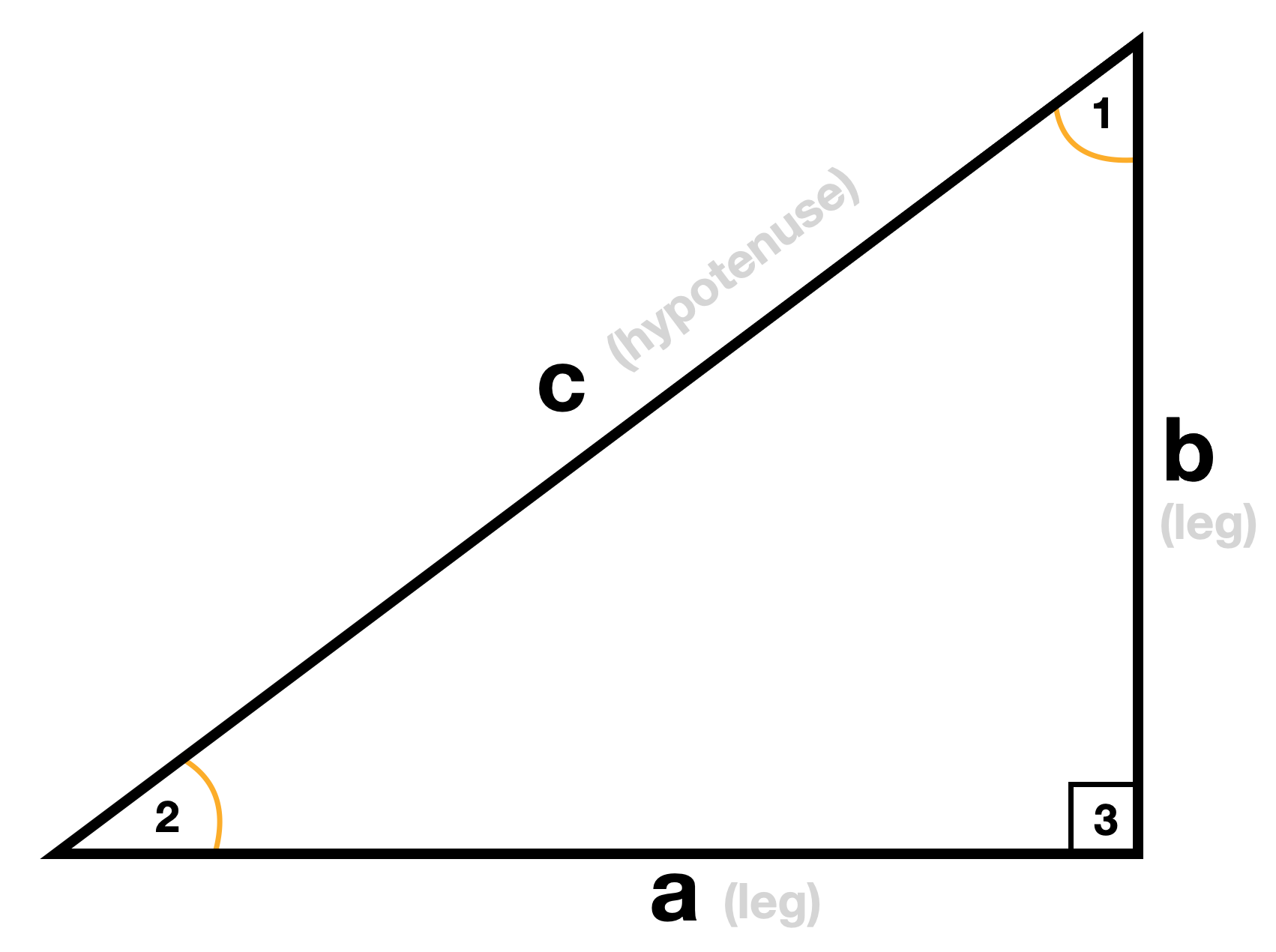
Right Triangle Calculator for the Hypotenuse is an educational tool designed to help students, teachers, and professionals in fields requiring geometric calculations. This calculator determines the length of the hypotenuse of a right triangle when the lengths of the other two sides are known. Understanding the hypotenuse is essential for various applications in mathematics, physics, engineering, and everyday problem solving.
How the Right Triangle Calculator Works
The calculator simplifies the process of finding the hypotenuse, the longest side of a right triangle, opposite the right angle, by utilizing the Pythagorean theorem.
Key Inputs:
- Side A: The length of one of the legs of the right triangle.
- Side B: The length of the other leg of the right triangle.
Formula Used:
The hypotenuse (C) is calculated using the Pythagorean theorem, which states:
C = sqrt(A^2 + B^2)Where:
- A and B are the lengths of the two legs.
- sqrt represents the square root function.
- A^2 and B^2 are the squares of the lengths of the legs.
General Terms and Definitions Table
| Term | Definition |
|---|---|
| Hypotenuse | The longest side of a right triangle, opposite the right angle. |
| Side A | One of the two shorter sides of the right triangle, perpendicular to Side B. |
| Side B | The other shorter side, perpendicular to Side A and adjacent to the right angle. |
| Right Triangle | A triangle in which one of the angles is a right angle (90 degrees). |
Example of Calculator Use
Scenario:
- Side A: 3 meters
- Side B: 4 meters
Calculation:
- Hypotenuse (C):
sqrt(3^2 + 4^2) = sqrt(9 + 16) = sqrt(25) = 5 meters
This example illustrates how the calculator determines that the hypotenuse of a right triangle with legs of 3 meters and 4 meters is 5 meters.
Most Common FAQs
1. Can the calculator handle any units of measurement?
Yes, the calculator can work with any units as long as both inputs are in the same unit (e.g., meters, feet, inches).
2. What should I do if I only know the hypotenuse and one leg?
You can rearrange the Pythagorean theorem to solve for the unknown leg: A = sqrt(C^2 - B^2) or B = sqrt(C^2 - A^2).
3. Is this calculator applicable to non-right triangles?
No, the Pythagorean theorem and this specific calculator apply only to right triangles.
4. How accurate is the calculator?
The accuracy depends on the precision of the input values. The mathematical calculations are precise and exact based on the Pythagorean theorem.
5. Can this tool help in real-world applications?
Absolutely. This calculator is useful for construction, carpentry, architecture, and anywhere spatial dimensions and right angles are involved.
The Right Triangle Calculator for Hypotenuse is a practical tool for quickly and accurately calculating the hypotenuse of right triangles, making it invaluable in educational settings and professional fields where quick geometric calculations are frequently required.






